AB 테스트 알아보기 - 1. 샘플 사이즈 계산 (with alpha, beta, power, critical value)

7 minute read

AB test는 판매량/전환율 등의 가설의 대상을 설정하고 실험군과 대조군을 나누어 데이터를 수집하고 두 집단의 통계량을 바탕으로 p value를 구해 새로운 기능 추가 등의 요소가 실제로 목표를 변화시켰냐를 검증해보는 방식으로 수행한다. 여기서 실험군과 대조군의 사이즈를 얼마나 정해야되는지를 Optimizely 같은 툴을 통해 정하고 실험을 설계하는데 개인적으로 이 샘플 사이즈를 정하는 로직을 처음에 이해하기가 어려웠다. 통계학 강의들과 여러 웹사이트들을 찾아보며 정리한 로직을 공유해보려 한다.

개요

샘플 사이즈 계산은 $\alpha$ 외에 $\beta$ 를 정해놓고 power(검정력)이 최소 0.8이 나올 수 있는 사이즈가 얼마냐를 정하는 방식으로 결정된다. 샘플 사이즈는 클수록 샘플의 분포가 평균에 가깝게 모여서 $\beta$ 가 낮아지기 때문에 power를 올려주게 된다. 이에 착안해 원하는 수치의 power(보통 0.8)을 최소로 확보하기 위한 숫자를 구하는 것이 샘플 사이즈 계산의 본질이다. 계산은 $\alpha$ 와 $\beta$ 에 따른 z 값과 $H_0$, $H_a$ 의 차이값을 통해 이루어진다.

결론적으로 가장 헷갈릴 수 있는 부분은 샘플 사이즈 결정에 $\alpha$ 외에 $\beta$ 가 함께 고려된다는 점이다. 여기서 $\alpha$ 는 $H_0$ 을 기각해도 된다고 판단할 확률로 일반적으로 p-value 계산이나 신뢰구간을 계산할 때 많이 고려되는데, 샘플 사이즈의 결정은 $\alpha$ 뿐만 아니라 $H_0$ 이 틀렸음에도 맞다고 판단하는 확률 $\beta$ 를 함께 고려해서 1종 오류와 2종 오류를 모두 고려해서 결정된다. 주로 $\beta$ 는 0.2를 고정으로 sample size calculator들이 계산되고 있어 설정값에 들어가지 않지만 실제로는 $\beta$ 를 변경해서도 사이즈를 계산할 수 있고 $\beta$ 가 고려된 수치이다.

개념 정리

아래 오류 분류 표를 보고 $\alpha$ 와 $\beta$ 에 대해 알아보자.

  $H_0$ 진실 $H_0$ 거짓
$H_0$ 기각 Type 1 Error ($\alpha$) Right Conclusion (1 - $\beta$)
$H_0$ 채택 Right Conclusion (1 - $\alpha$) Type 2 Error ($\beta$)

$\alpha$

표를 바탕으로 생각해보면 $\alpha$ 는 $H_0$ 이 진실일 때 이를 잘못 기각할 확률이 얼마이냐를 의미한다.

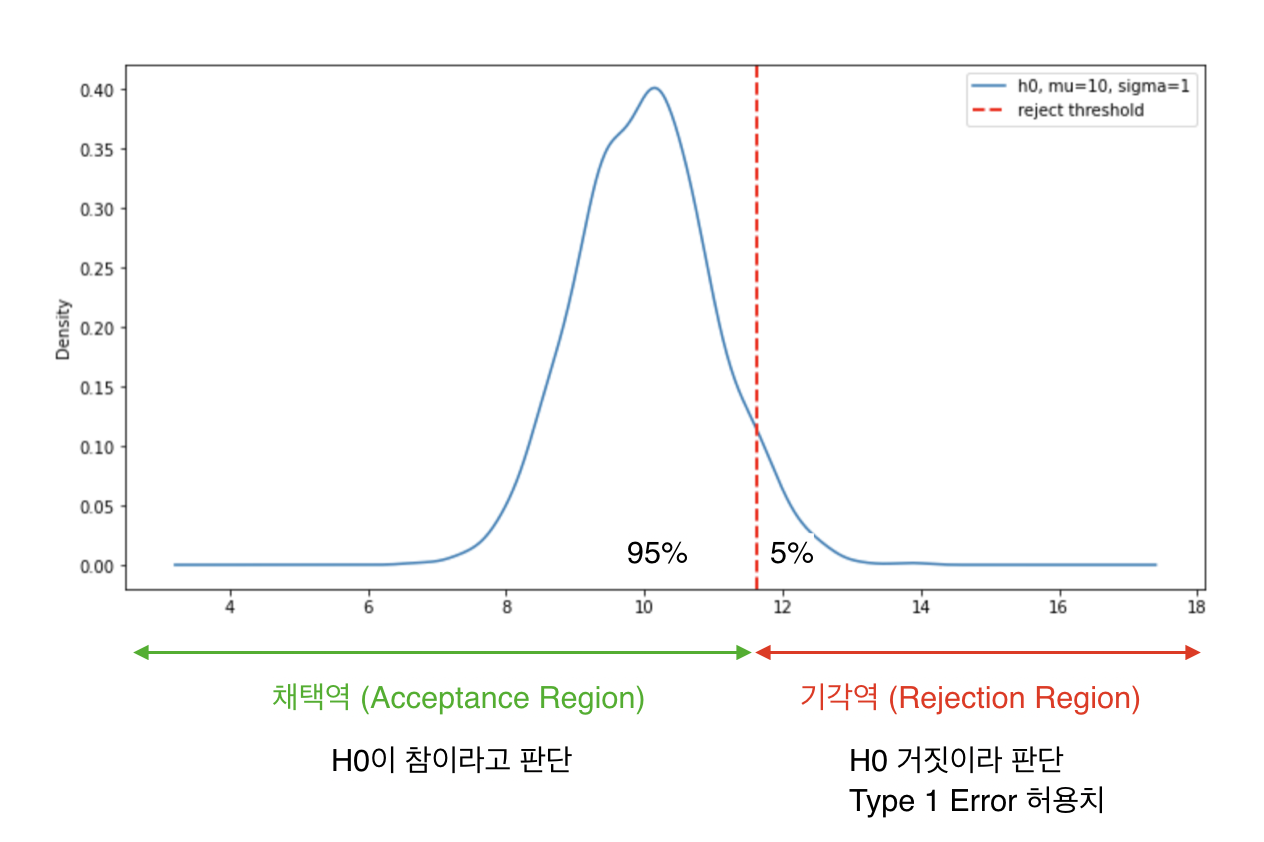
꽤 헷갈리는 개념인데 우리가 이 값을 지정하고 통계 분석을 진행한다는 점을 생각해보면 이해가 쉽다. 흔히 사용하는 0.05를 $\alpha$ 로 지정하면 평균을 기준으로 95% 신뢰구간의 값이 넘어가는 범위의 값들이 나올 때 $H_0$ 을 기각하게 되는데 이 때 5% 확률로는 이 값들도 $H_0$ 분포에서 나온 값일 수도 있으므로 그만큼의 Type 1 Error가 발생하게 된다. ($a<=x<=b$ 로 구해진 신뢰구간은 분포에서 그 범위 안의 값들이 나올 확률이 95%를 의미)

AB 테스트에서는 위에서 말한 것처럼 $H_0$ 을 기각할 때 어느정도로 Type 1 Error을 허락할 확률을 정하는 관점에서 0.05, 0.01 등의 값을 사용한다.

/assets/images//abtest-alpha.png

$\beta$

$\beta$ 는 $H_0$ 이 틀렸을 때 이를 맞다고 판단할 확률이다.

이는 그림을 통해 이해하면 쉽다.

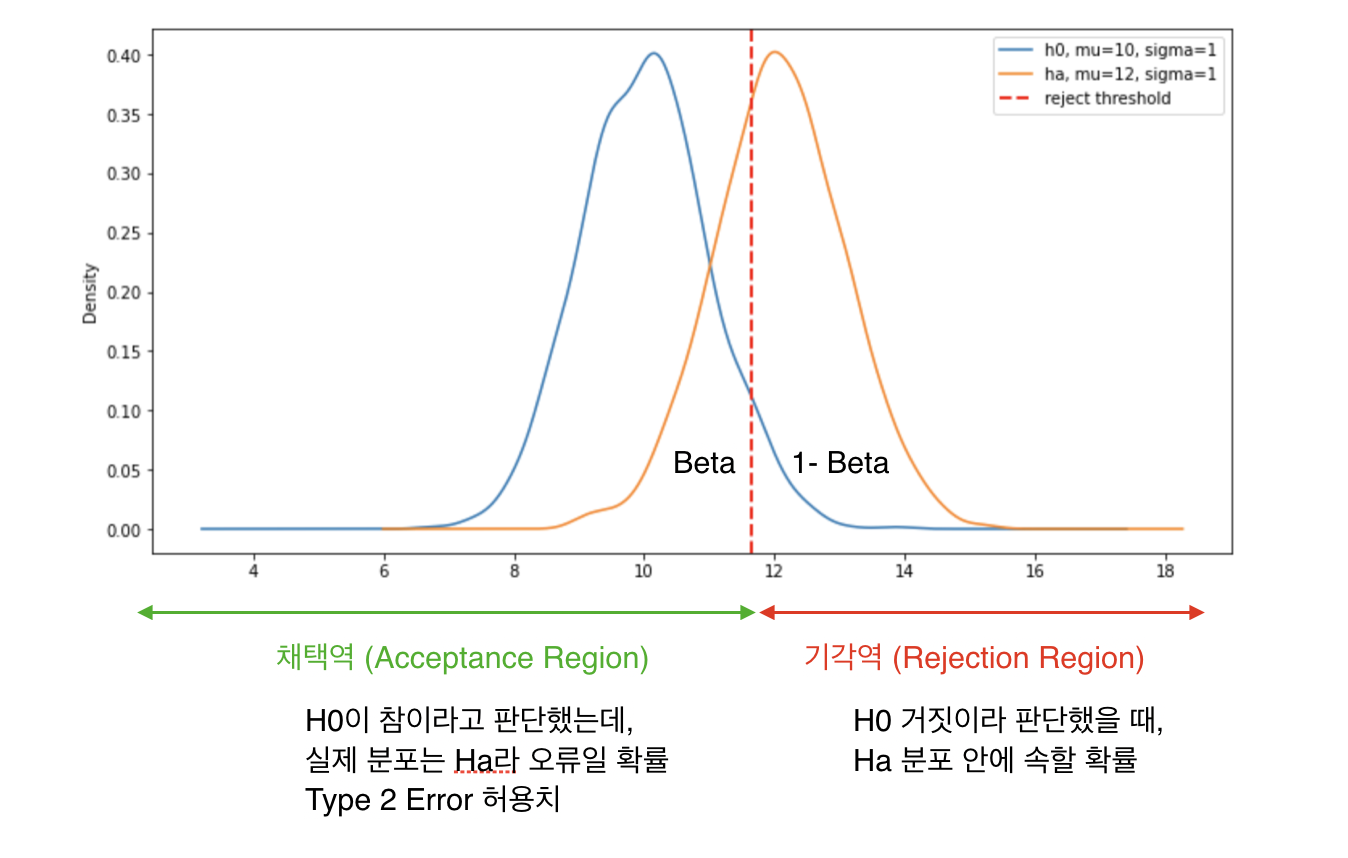
/assets/images//abtest-beta.png

$H_0$ 의 신뢰구간 안(그림에서는 채택역으로 표시된 영역)에 $H_a$ 의 분포가 포함될 확률이다. $\beta$ 는 $\alpha$ 이후에 생각되는 개념이라 $\alpha$ 를 기준으로 채택/기각의 기준이 되는 영역이 정해지고 그 후에 그 영역과 $H_a$ 분포를 바탕으로 $\beta$ 가 계산된다고 생각하면 된다.

AB 테스트에서는 1 - $\beta$ 의 값인 power를 기준으로 관습적으로 0.8을 주로 사용한다. 여기서 의미는 $H_0$ 이 틀렸을 때 이를 틀리다고 할 확률을 80%로 놓고 실험을 진행하겠다는 뜻이다.

$H_0$, $H_a$

AB 테스트에서 $H_0$ 과 $H_a$ 는 아래와 같다.

$H_0 = \mu_a - \mu_b =0$

$H_a = \mu_a - \mu_b !=0 \ \ or \ \ H_a = \mu_a - \mu_b >0 \ \ or \ \ H_a = \mu_a - \mu_b <0$

원하는 $H_a$ 는 설정하기 나름이지만 보통 $H_a = \mu_a - \mu_b > 0$ 로 새로 바뀐 사이트가 전환율/매출 등을 올렸냐를 기준으로 설정하게 된다. 이는 one-tailed 케이스로 단순히 같지 않다로 양쪽을 비교하는 two-tailed 케이스와 달리 한 쪽으로 5%든 1%든 $\alpha$ 에 해당하는 z 값을 구해서 사용한다. 여기서 $H_0$ 은 A군과 B군 두 개가 차이가 없음을 의미하는 $H_0 = \mu_a - \mu_b =0$ 이 된다. A군과 B군을 비교하는 것이 아니라 두 개의 차이값을 바탕으로 $H_0$ 과 $H_a$ 를 구성한다는 점을 기억해야 한다.

실험 설계 전 적절한 샘플 사이즈를 구할 때는 $\mu_a$ 를 과거 데이터로부터 확인하고 그 값을 baseline으로 삼고 계산하게 된다.

Minimum Detectable Effect

실제 적절한 샘플 사이즈를 바탕으로 한 AB 테스트에서는 p value를 통해 두 분포가 유의미한 차이가 있다를 확인하고 두 분포 사이의 uplift를 계산해 얼마만큼의 개선이 일어났나를 본다. 하지만 단순 조금 더 전환율이 올라간다보다 10%의 전환율에서 최소 3%의 차이가 나는 지를 확인하고 싶다면 minimum detectable effect를 고려해서 샘플 사이즈를 계산해야 한다. 보통 relative한 수치를 사용하며 10% 전환율에서 3% 차이를 확인하려면 30%로 수치를 설정한다.

샘플 사이즈 계산 방식에서는 MDE를 바탕으로 $H_a$의 분포를 구하고 $H_0$과의 비교를 통해 power를 구한다.

$\mu(n_a, A) - \mu(n_b, B) \sim N(\mu_b - \mu_a, \frac{\sigma_b^{2}}{n_b} + \frac{\sigma_a^{2}}{n_a})$

중심극한정리(Central Limit Theorem)에 따라 실험을 적절하게 설계했다면 $\mu(n_a, A) \sim N(\mu_a, \frac{\sigma_a^{2}}{n_a})$, $\mu(n_b, B) \sim N(\mu_a, \frac{\sigma_b^{2}}{n_b})$ 가 성립한다. 우리가 구해야할 분포는 $\mu(n_a, A) - \mu(n_b, B)$ 인데 분산의 경우 두 분산 간의 차이를 볼 때에도 합해진 값으로 분산이 계산된다. 따라서 위에 식처럼 $\frac{\sigma_b^{2}}{n_b} + \frac{\sigma_a^{2}}{n_a}$ 으로 분산이 구해진다. 두 개의 극단적으로 다른 분포의 차이를 보게 되면 떨어진 정도가 줄어드는 것이 아니라 늘어날 것이라는 직관으로 더해지는 분산을 이해하면 좋을 것 같다.

참고로 $H_0$ 이 참일 때 $\mu(n_a, A) - \mu(n_b, B) \sim N(0, \frac{\sigma_b^{2}}{n_b} + \frac{\sigma_a^{2}}{n_a})$ 이 되는데 다시 풀어서 쓰면 $\frac{\mu(n_a, A) - \mu(n_b, B)}{\sqrt{\frac{\sigma_b^{2}}{n_b} + \frac{\sigma_a^{2}}{n_a}}} \sim N(0, 1)$ 으로 z score를 사용할 수 있는 (0, 1) 정규분포를 따른다고 볼 수 있다.

계산

계산은 문제가 continous에 관한 문제이냐 propotion에 관한 문제이냐에 따라 조금 다르다. 하지만 그 원리는 비슷하다.

샘플 사이즈 계산에서 우리가 input으로 쓰는 값은 $\alpha$, $\beta$, $\mu_0$, $\mu_a$ 이다. 계산은 정해진 $\alpha$ 와 $\beta$ 값을 구하는 수식을 이용하면 된다.

$H_0 = \mu_a - \mu_b =0$

$H_a = \mu_a - \mu_b >0$

인 경우를 가정해보겠다.

Continuous Mean

위 $\beta$ 그림에서 기각역과 채택역을 나누는 threshold를 k라 하고 샘플의 random variable을 $\bar Y$ 라 해보자. 이 때 $\alpha$ 와 $\beta$ 는 아래와 같이 계산될 수 있다.

$\alpha = P(\bar{Y} > k, \mu=\mu_0) = P(Z > \frac{k-\mu_0}{\sigma / \sqrt{n}}, \mu=\mu_0)= P(Z > z_\alpha)$

$\beta = P(\bar{Y} <= k, \mu=\mu_a) = P(Z <= \frac{k-\mu_{a}}{\sigma / \sqrt{n}}, \mu=\mu_{a}) = P(Z <= -z_\beta)$

여기서 우리는 $\alpha = 0.05$, $\beta = 0.2$ 로 만드는 $z_\alpha$ 와 $z_\beta$ 를 구할 수 있다. ($z_\beta$ 는 (0, 1) 분포로 바꿨을 때 마이너스로 되는 왼쪽 부분을 봐야 하므로 위 같은 식으로 표현)

k를 공통으로 수식을 다시 전개하면

$k = \mu_0 + z_\alpha(\frac{\sigma}{\sqrt{n}}) = \mu_a + z_\beta(\frac{\sigma}{\sqrt{n}})$ 이 된다.

n으로 다시 정리하면

$n = \frac{(z_\alpha + z_\beta)^2\sigma^2}{(\mu_a - \mu_0)^2}$ 이 된다.

$\beta$ 가 0.2일 때 $z_\beta$ 는 0.84이고, one-tailed 케이스이므로 $\alpha$ 0.05일 때 $z_\alpha$ 는 1.64이다.

Continuous 케이스의 경우에는 사이트 체류시간이 5분에서 6분으로 늘었다든지 하는 케이스를 점검하게 된다. 이 때 continous는 실험 설계 전에 따로 $\sigma$ 를 구할 방법이 없어 직접 임의의 값을 넣어서 계산해야 한다.

Proportion

Continous와 같은 식을 사용하는데 proportion의 경우 standard deviation을 몰라도 조건을 맞추면 $\sigma^2 = p_0(1-p_0) + p_a(1-p_a)$ 로 standard deviation을 구할 수 있다.

이를 식에 적용하면

$n = \frac{(z_\alpha + z_\beta)^2(p_0(1-p_0) + p_a(1-p_a))^2}{(p_a - p_0)^2}$ 으로 만들 수 있다.

예를 들어 원래 전환율이 2%이고 최소 0.2%의 전환율 상승(MDE = 0.1)을 $\alpha=0.05 (z_\alpha=1.64), \ \beta=0.8 (z_\beta=0.84)$ 아래에서 구하고 싶다고 한다고 가정해보자. 이를 위 수식에 적용하면 아래와 같이 작성되고 63219의 값이 나온다.

>>> ((0.84 + 1.64)**2 * ((0.02)*(1-0.02) + (0.022)*(1-0.022))) / (0.022 - 0.02) **2
63219.96160000011

만약 $H_a = \mu_a - \mu_b >0$ 인 케이스가 아닌 $H_a = \mu_a - \mu_b !=0$ 인 케이스를 테스트하고 싶다면 분포의 양쪽을 봐야해서 $z_\alpha$ 값이 1.96으로 바뀐다. 이 때 계산을 다시 하면 80587로 다른 값이 나오게 된다.

>>> ((0.84 + 1.96)**2 * ((0.02)*(1-0.02) + (0.022)*(1-0.022))) / (0.022 - 0.02) **2
80587.36000000012

그림으로 보는 샘플 사이즈 결정

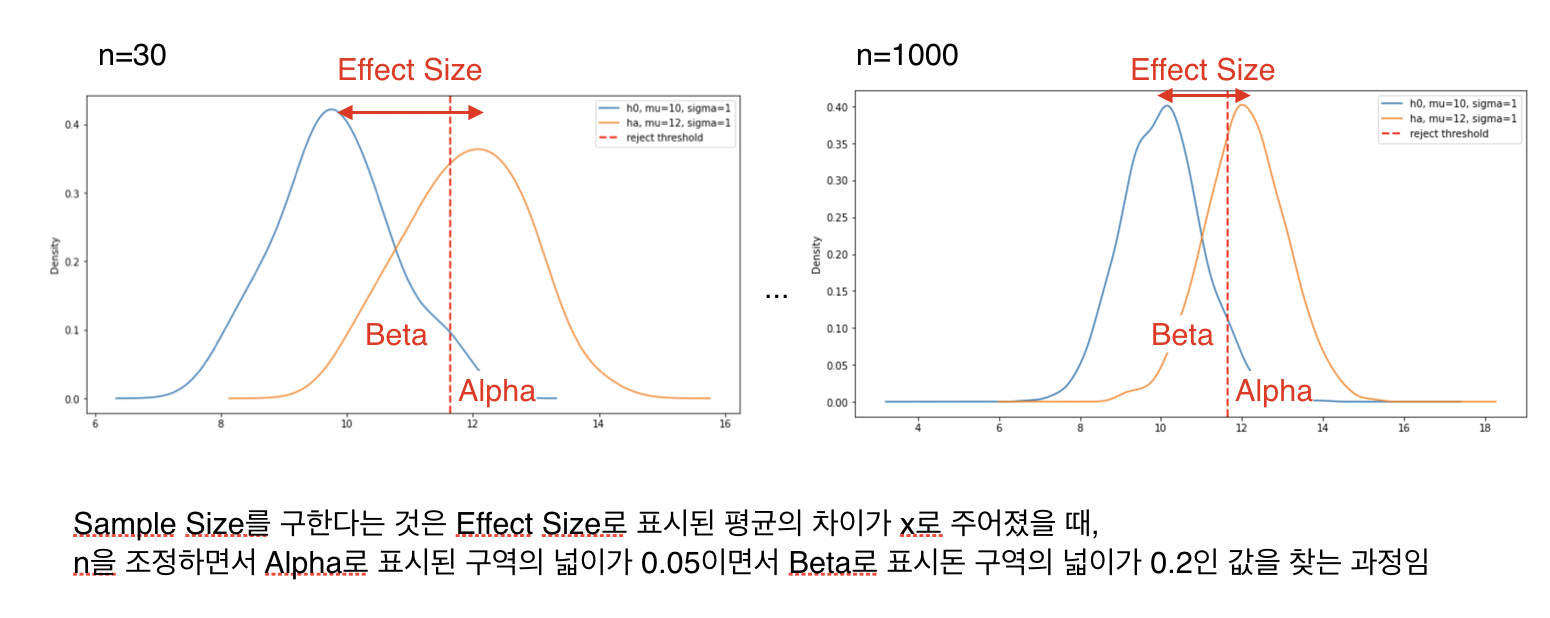
/assets/images//abtest-sample-intuition.png

수식으로 전개한 샘플 사이즈 n을 구하는 방식은 그림으로 보면 위와 같다. 그래프를 그릴 때 scale이 조금 달라져서 크기는 다르지만 effect size는 동일한 상태에서 n을 높일수록 분포가 평균에 모이게 되어 $\beta$ 값이 작아지게 된다. effect size와 $\alpha$ 가 고정된 상태에서 n에 따라 $\beta$ 가 변하게 되는데 샘플 사이즈 결정은 샘플을 높여가면서 $\beta$ 가 0.2가 되는 최소 n을 찾는 과정이다.

이를 다른 식으로 생각해보면 n, $\alpha$, $\beta$ 를 고정해 minimum defectable effect size를 계산하는 것도 가능하다.

샘플 사이즈와 AB 테스트 기간 설정

샘플 사이즈와 연관되 AB 테스트의 기간을 설정하는 문제가 있다. 가장 단순하게는 위에서 샘플 사이즈 / 일평균방문자수 로 구할 수 있다. 다만, 실제 실험 설계 시에는 방문자수가 많아 3일 정도의 기간이 나왔다 하더라도 주중과 주말의 유저 행동 패턴 차이점 등을 고려해 모든 요일이 포함되는 최소 일주일을 고려한다든가 특정 주말의 아웃라이어를 줄이기 위해 2주를 사용한다든가 하는 식으로 기간을 설정할 수 있다.

Margin of Error와 관련된 Sample Size 계산

샘플 사이즈 계산 중에 margin of error를 특정 범위로 정해서 구하는 샘플 사이즈가 있다. 이 샘플 사이즈는 위에서 말한 AB test 상황과 달리 모집단(population)에서 어떤 갯수의 표본을 뽑아야 신뢰구간에 기반한 margin of error가 $\pm 2%$ 같은 범위 안에 속할 수 있게 뽑을 수 있냐를 정하는 샘플 사이즈이다. 이에 대한 설명은 아래 칸아카데미 동영상을 첨부한다.

https://www.khanacademy.org/math/ap-statistics/xfb5d8e68:inference-categorical-proportions/one-sample-z-interval-proportion/v/determining-sample-size-based-on-confidence-and-margin-of-error

마치며

AB 테스트 샘플 사이즈를 구하는 방법에 대해 알아보았다. Calculator에 따라 $\beta$ 값을 얼마나 정확하게 쓰냐 아니면 one-tail인지 two-tail인지 어디서 반올림하는 지에 따라 결과가 조금씩 다르게 나올 수 있다. 계산 공식은 https://greeksharifa.github.io/machine_learning/2021/09/30/sample-size/을 많이 참조했다. https://ytliu0.github.io/Stat_Med/power2.html 에는 sample size calculator를 다양하게 simulation할 수 있도록 만들었는데 n이 커질수록 어떤 식으로 power가 변하고 하는 지를 좀 더 자세하게 알아볼 수 있어 참조 링크로 추가했다. 이번 포스트가 샘플 사이즈 계산 이해에 조금이라도 도움이 되는 글이 되었으면 한다.

References

Leave a comment

You may also enjoy